classification(2) -- NIN、BatchNorm、Highway、PReLU
paper: Network In Network
Contributions
- mlpconv layer
- global average pooling
Architecture

The cross channel parametric pooling layer can be seen as a convolution layer with 1x1 convolution kernel.
Why using multilayer perceptron ?
- multilayer perceptron is compatible with the structure of convolutional neural networks, which is trained using back-propagation.
- multilayer perceptron can be a deep model itself, which is consistent with the spirit of feature re-use.
Why global average pooling ?
- it is more native to the convolution structure by enforcing correspondences between feature maps and categories.
- there is no parameter to optimize in the global average pooling thus overfitting is avoided at this layer.
- global average pooling sums out the spatial information, thus it is more robust to spatial translations of the input.
Other details are in the paper.
paper: Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
internal covariate shift problem: the distribution of each layer’s inputs changes during training, as the parameters of the previous layers change. This slows down the training by requiring lower learning rates and careful parameter initialization, and makes it notoriously hard to train models with saturating nonlinearities.
Algorithm

Normalize each scalar feature independently,by making it have the mean of zero and the variance of 1. but this may change what the layer can represent. To address this, it should make sure that the transformation inserted in the network can represent the identity transform. γ and β which can scale and shift the normalized value are to be learned.
How it work
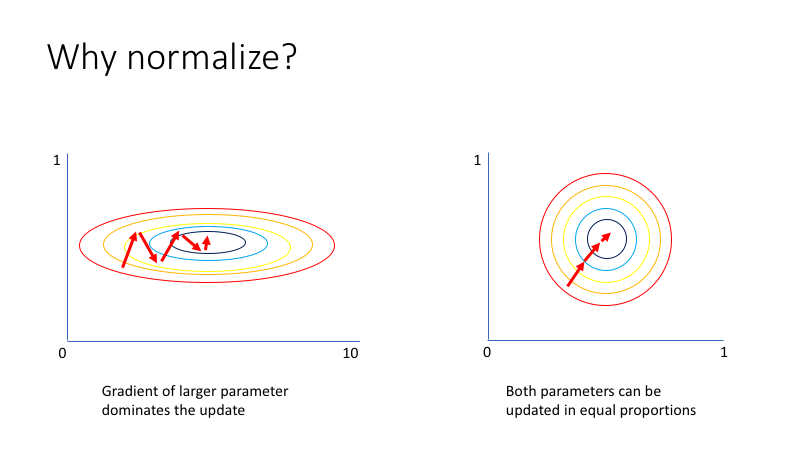
- allowing us to use much higher learning rates without the risk of divergence can make learning faster.
- regularizes the model and reduces the need for Dropout
- make it possible to use saturating nonlinearities by preventing the network from getting stuck in the saturated modes
Batch-Normalized Convolutional Networks
- the bias b can be ignoredsince its effect will be canceled by the subsequent mean subtraction. Thus,
z = g(W*u + b)is replaced withz = g(BN(W*u)) - suppose input feature map size is (batch_size, channel, weight, height), it’s a channel-wise normalization.
paper: Highway Networks
It is well known that deep networks can represent certain function classes exponentially more efficiently than shallow ones. However, network training becomes more difficult with increasing depth and training of very deep networks. Inspired by LSTM, highway networks actually utilize the gating mechanism to pass information almost unchanged through many layers.
Architecture
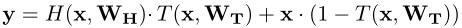
the transform gate defined as:
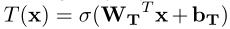
so:
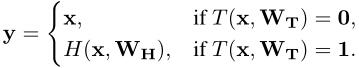
- H(x) and T(x) are the same dimension.
- use a plain layer (without highways) to change dimensionality and then continue with stacking highway layers.
- bT can be initialized with a negative value (e.g. -1, -3 etc.)
- highway networks performs better than plain networks when networks go deeper.
paper: Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification
Parametric Rectified Linear Unit (PReLU)
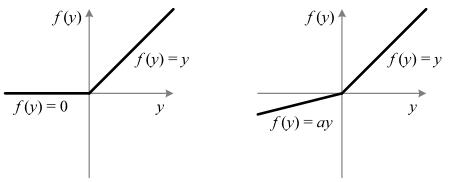
Above is ReLU vs. PReLU, a is a coefficient controlling the slope of the negative part and a learnable parameter.
two interesting phenomena:
- First, the first conv layer (conv1) has coefficients (0.681 and 0.596) significantly greater than 0. As the filters of conv1 are mostly Gabor-like filters such as edge or texture detectors, the learned results show that both positive and negative responses of the filters are respected.
- Second, for the channel-wise version, the deeper conv layers in general have smaller coefficients. This implies that
the activations gradually become “more nonlinear” at increasing depths. In other words, the learned model tends to keep more information in earlier stages and becomes more discriminative in deeper stages.
notice:
- do not use weight decay (l2 regularization) when updating a. A weight decay tends to push a to zero, and thus biases PReLU toward ReLU. Even without regularization, the learned coefficients rarely have a magnitude larger than 1 in our experiments.
- do not constrain the range of a so that the activation function may be non-monotonic.
- We use a = 0.25 as the initialization.
He’s initialization method
a zero-mean Gaussian distribution whose standard deviation (std) is np.sqrt(2/n) and bias to 0.